Skip to content

第十五讲：子空间投影

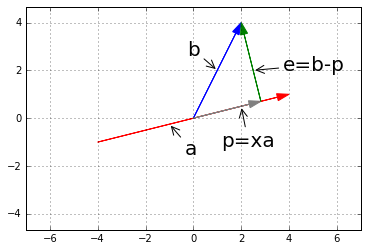
从\(\mathbb{R}^2\)空间讲起，有向量\(a, b\)，做\(b\)在\(a\)上的投影\(p\)，如图：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

plt.style.use("seaborn-dark-palette")

fig = plt.figure()
plt.axis('equal')
plt.axis([-7, 7, -6, 6])
plt.arrow(-4, -1, 8, 2, head_width=0.3, head_length=0.5, color='r', length_includes_head=True)
plt.arrow(0, 0, 2, 4, head_width=0.3, head_length=0.5, color='b', length_includes_head=True)
plt.arrow(0, 0, 48/17, 12/17, head_width=0.3, head_length=0.5, color='gray', length_includes_head=True)
plt.arrow(48/17, 12/17, 2-48/17, 4-12/17, head_width=0.3, head_length=0.5, color='g', length_includes_head=True)
# plt.plot([48/17], [12/17], 'o')
# y=1/4x
# y=-4x+12
# x=48/17
# y=12/17
plt.annotate('b', xy=(1, 2), xytext=(-30, 15), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('a', xy=(-1, -0.25), xytext=(15, -30), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('e=b-p', xy=(2.5, 2), xytext=(30, 0), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.annotate('p=xa', xy=(2, 0.5), xytext=(-20, -40), textcoords='offset points', size=20, arrowprops=dict(arrowstyle="->"))
plt.grid()

png

plt.close(fig)

从图中我们知道，向量\(e\)就像是向量\(b, p\)之间的误差，\(e=b-p, e \bot p\)。\(p\)在\(a\)上，有\(\underline{p=ax}\)。

所以有\(a^Te=a^T(b-p)=a^T(b-ax)=0\)。关于正交的最重要的方程：

\[ a^T(b-xa)=0 \\ \underline{xa^Ta=a^Tb} \\ \underline{x=\frac{a^Tb}{a^Ta}} \\ p=a\frac{a^Tb}{a^Ta} \]

从上面的式子可以看出，如果将\(b\)变为\(2b\)则\(p\)也会翻倍，如果将\(a\)变为\(2a\)则\(p\)不变。

设投影矩阵为\(P\)，则可以说投影矩阵作用与某个向量后，得到其投影向量，\(projection_p=Pb\)。

易看出\(\underline{P=\frac{aa^T}{a^Ta}}\)，若\(a\)是\(n\)维列向量，则\(P\)是一个\(n \times n\)矩阵。

观察投影矩阵\(P\)的列空间，\(C(P)\)是一条通过\(a\)的直线，而\(rank(P)=1\)（一列乘以一行：\(aa^T\)，而这一列向量\(a\)是该矩阵的基）。

投影矩阵的性质：

  • \(\underline{P=P^T}\)，投影矩阵是一个对称矩阵。
  • 如果对一个向量做两次投影，即\(PPb\)，则其结果仍然与\(Pb\)相同，也就是\(\underline{P^2=P}\)。

为什么我们需要投影？因为就像上一讲中提到的，有些时候\(Ax=b\)无解，我们只能求出最接近的那个解。

\(Ax\)总是在\(A\)的列空间中，而\(b\)却不一定，这是问题所在，所以我们可以将\(b\)变为\(A\)的列空间中最接近的那个向量，即将无解的\(Ax=b\)变为求有解的\(A\hat{x}=p\)（\(p\)是\(b\)在\(A\)的列空间中的投影，\(\hat{x}\)不再是那个不存在的\(x\)，而是最接近的解）。

现在来看\(\mathbb{R}^3\)中的情形，将向量\(b\)投影在平面\(A\)上。同样的，\(p\)是向量\(b\)在平面\(A\)上的投影，\(e\)是垂直于平面\(A\)的向量，即\(b\)在平面\(A\)法方向的分量。 设平面\(A\)的一组基为\(a_1, a_2\)，则投影向量\(p=\hat{x_1}a_1+\hat{x_2}a_2\)，我们更倾向于写作\(p=A\hat{x}\)，这里如果我们求出\(\hat{x}\)，则该解就是无解方程组最近似的解。

现在问题的关键在于找\(e=b-A\hat{x}\)，使它垂直于平面，因此我们得到两个方程 $ \begin{cases}a_1^T(b-A\hat{x})=0\ a_2^T(b-A\hat{x})=0\end{cases} $，将方程组写成矩阵形式 $ \begin{bmatrix}a_1^T\a_2^T\end{bmatrix} (b-A\hat{x})= \begin{bmatrix}0\0\end{bmatrix} \(，即\)A^T(b-A\hat{x})=0$。

比较该方程与\(\mathbb{R}^2\)中的投影方程，发现只是向量\(a\)变为矩阵\(A\)而已，本质上就是\(A^Te=0\)。所以，\(e\)在\(A^T\)的零空间中（\(e\in N(A^T)\)），从前面几讲我们知道，左零空间\(\bot\)列空间，则有\(e\bot C(A)\)，与我们设想的一致。

再化简方程得\(A^TAx=A^Tb\)，比较在\(\mathbb{R}^2\)中的情形，\(a^Ta\)是一个数字而\(A^TA\)是一个\(n\)阶方阵，而解出的\(x\)可以看做两个数字的比值。现在在\(\mathbb{R}^3\)中，我们需要再次考虑：什么是\(\hat{x}\)？投影是什么？投影矩阵又是什么？

  • 第一个问题：\(\hat x=(A^TA)^{-1}A^Tb\)；
  • 第二个问题：\(p=A\hat x=\underline{A(A^TA)^{-1}A^T}b\)，回忆在\(\mathbb{R}^2\)中的情形，下划线部分就是原来的\(\frac{aa^T}{a^Ta}\)；
  • 第三个问题：易看出投影矩阵就是下划线部分\(P=A(A^TA)^{-1}A^T\)。

这里还需要注意一个问题，\(P=A(A^TA)^{-1}A^T\)是不能继续化简为\(P=AA^{-1}(A^T)^{-1}A^T=I\)的，因为这里的\(A\)并不是一个可逆方阵。 也可以换一种思路，如果\(A\)是一个\(n\)阶可逆方阵，则\(A\)的列空间是整个\(\mathbb{R}^n\)空间，于是\(b\)在\(\mathbb{R}^n\)上的投影矩阵确实变为了\(I\)，因为\(b\)已经在空间中了，其投影不再改变。

再来看投影矩阵\(P\)的性质： * \(P=P^T\)：有 $ \left[A(A^TA)^{-1}A^T\right]^T=A\left[(A^TA)^{-1}\right]^TA^T \(，而\)(A^TA)\(是对称的，所以其逆也是对称的，所以有\)A((A^TA)^{-1})^TA^T=A(A^TA)^{-1}A^T$，得证。 * \(P^2=P\)：有 $ \left[A(A^TA)^{-1}A^T\right]\left[A(A^TA)^{-1}A^T\right]=A(A^TA)^{-1}\left[(A^TA)(A^TA)^{-1}\right]A^T=A(A^TA)^{-1}A^T $，得证。

最小二乘法

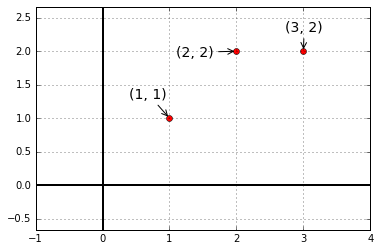
接下看看投影的经典应用案例：最小二乘法拟合直线（least squares fitting by a line）。

我们需要找到距离图中三个点 \((1, 1), (2, 2), (3, 2)\) 偏差最小的直线：\(b=C+Dt\)。

plt.style.use("seaborn-dark-palette")

fig = plt.figure()
plt.axis('equal')
plt.axis([-1, 4, -1, 3])
plt.axhline(y=0, c='black', lw='2')
plt.axvline(x=0, c='black', lw='2')

plt.plot(1, 1, 'o', c='r')
plt.plot(2, 2, 'o', c='r')
plt.plot(3, 2, 'o', c='r')

plt.annotate('(1, 1)', xy=(1, 1), xytext=(-40, 20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('(2, 2)', xy=(2, 2), xytext=(-60, -5), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))
plt.annotate('(3, 2)', xy=(3, 2), xytext=(-18, 20), textcoords='offset points', size=14, arrowprops=dict(arrowstyle="->"))

plt.grid()

png

plt.close(fig)

根据条件可以得到方程组 $ \begin{cases} C+D&=1 \ C+2D&=2 \ C+3D&=2 \ \end{cases} \(，写作矩阵形式 \(\begin{bmatrix}1&1 \\1&2 \\1&3\\\end{bmatrix}\begin{bmatrix}C\\D\\\end{bmatrix}=\begin{bmatrix}1\\2\\2\\\end{bmatrix}\)，也就是我们的\)Ax=b\(，很明显方程组无解。但是\)A^TA\hat x=A^Tb\(有解，于是我们将原是两边同时乘以\)A^T\(后得到的新方程组是有解的，\)A^TA\hat x=A^Tb$也是最小二乘法的核心方程。

下一讲将进行最小二乘法的验算。

回到顶部